Metr kwadratowy powierzchni pokoju to ile i jak szybko obliczyć?
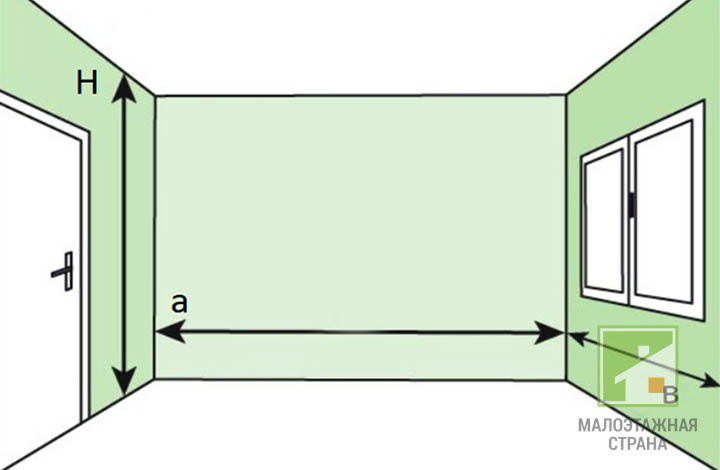
Metr kwadratowy to jednostka miary, która reprezentuje iloczyn dwóch wartości liczbowych dla długości i szerokości obiektu. Innymi słowy, długość jest mnożona przez szerokość. Otrzymany wynik ma swój własny termin matematyczny - pole powierzchni lub charakterystykę numeryczną płaszczyzny (w przeciwieństwie do objętości - charakterystyka ilościowa przestrzeni). Najczęściej takie parametry spotyka się przy obliczaniu powierzchni pokoju, działki, ilości zużycia materiałów budowlanych. Metry kwadratowe można obliczyć na różne sposoby, które zostaną omówione poniżej.
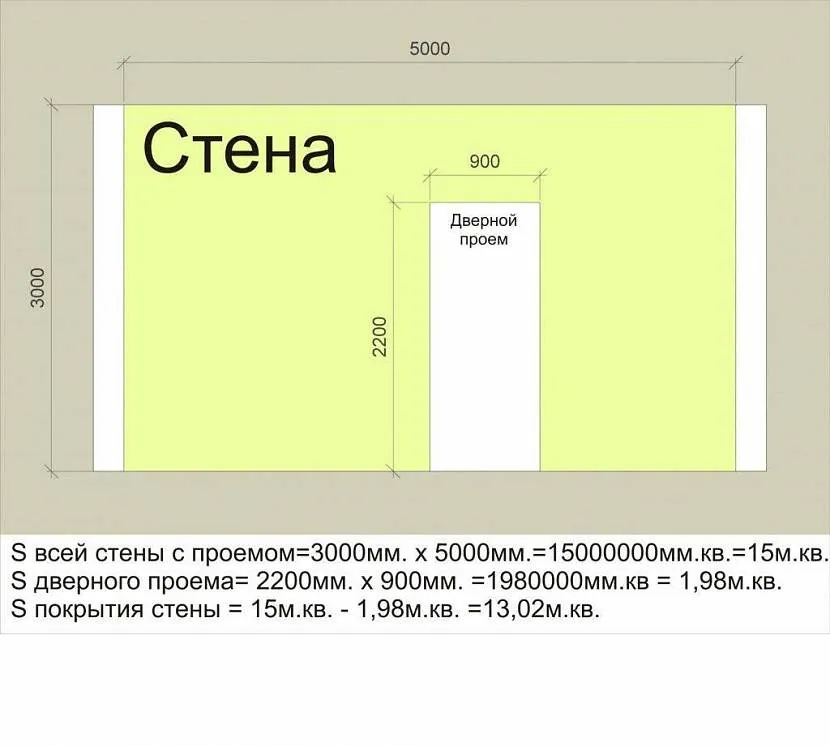
Obliczanie metrów kwadratowych powierzchni
Do obliczeń potrzebna będzie centymetrowa taśma miernicza lub taśma miernicza. Za ich pomocą dokonuje się pomiarów boków figury geometrycznej o odpowiednim kształcie (prostokąt, kwadrat i inne opcje). Wtedy wszystko się mnoży. Po uzyskanych wynikach centymetry należy przeliczyć na metry.
Algorytm:
- Weź taśmę mierniczą lub taśmę mierniczą, na płótnie której podziały są stosowane w tym samym systemie miar - centymetry lub metry.
- Zmierz długość obiektu w przestrzeni dwuwymiarowej - płaszczyźnie.
- Zmierz szerokość obiektu. Krawędź przyrządu pomiarowego o wartości zerowej jest umieszczona pod kątem 90° w stosunku do długości w narożniku figury.
- Jeśli nie można wykonać pomiaru za jednym razem, zmierz część płaszczyzny do końca taśmy mierniczej (taśmy), umieść znak ołówkiem lub markerem, zacznij od niego mierzyć następny odcinek. Przejdź do końca całej długości lub szerokości. Zapisz liczby i dodaj je.
- Zapisz wszystkie uzyskane wartości.
- Cyfrową wartość długości za pomocą kalkulatora mnoży się przez cyfrową wartość szerokości - otrzymuje się liczbę wskazującą powierzchnię.
Przykład:
Długość - 3,42 m²
Szerokość - 2,15 m²
3,42 x 2,15 = 7353
Zaokrąglamy w górę do liczby dwucyfrowej po przecinku - 7,35 metra kwadratowego. m
Często wynik nie jest przedstawiany jako liczba całkowita – odzwierciedla zarówno metry, jak i centymetry. Dlatego musisz przeliczyć centymetry na metry. Wtedy łatwiej będzie pomnożyć liczby. Przykład: 3 metry 78 centymetrów. Jeden centymetr to 0,01 metra. Tłumaczenie odbywa się prostą techniką - przesuwając przecinek liczby „0,01” o 2 cyfry do tyłu (w lewo).
Przykład obliczenia:
78 cm = 0,78 m²
3m 78cm = 3m + 78cm = 3,78m
Jeśli weźmiesz taśmę mierniczą lub taśmę mierniczą, oczywiście łatwiej będzie policzyć - nie musisz konwertować uzyskanych wartości liczbowych na metry. Pomiary długości, szerokości wykonuje się od jednego punktu (narożnika) do drugiego, przeciwległego punktu (narożnik). Jeśli wynik nie jest liczbą całkowitą, liczone są nie tylko metry, ale także centymetry. Przykład: 3,55 m - 3 metry i 55 centymetrów.

Gdy liczby są mniejsze niż jeden metr w milimetrach, zaokrąglają się do najbliższego centymetra. Przykład: 2 metry 4 centymetry i 3 milimetry są rejestrowane jako 2,4 m. Ale podczas instalowania ramy meblowej ważna jest absolutna dokładność. Dlatego wszystko jest tutaj weryfikowane na milimetry. Dotyczy to zwłaszcza szafek wbudowanych w nisze ścienne.
Konwersja innych jednostek powierzchni
Zagraniczne jednostki miary oznaczają również metr kwadratowy. Tylko w tym celu należy je poprawnie przekonwertować. Można to zrobić za pomocą prostego obliczenia matematycznego:
- Stopy kwadratowe — pomnóż przez 0,093 (dokładna stawka to 0,093903). Zmierz długość i szerokość w stopach i pomnóż je. Zdobądź stopę kwadratową. Jedna stopa to 0,093 metra kwadratowego. Wynik uzyskany w stopach kwadratowych mnoży się przez 0,093 i otrzymuje się metr kwadratowy. Przykład: 13,41 stopy x 0,093 = 1,24713 kw. m. Zaokrąglanie - 1,25 tys. m.
- Jardy - pomnóż przez 0,84 (dokładny kurs - 0,83613). Wszyscy robią to samo, co przy przeliczaniu stóp kwadratowych na metry kwadratowe. Przykład: 24,7 jardów x 0,84 = 20,748 kw. m. Zaokrąglanie - 20,75 mkw. m.
- Akry - pomnóż przez 4050 (dokładna stawka - 4046,9). Powtarzamy procedurę. Przykład: 55,3 akrów x 4050 = 224014,77 mkw. m. Zaokrąglanie - 224015 tys. m.
Ilościowe wartości stóp lub jardów zawsze wydają się większe niż metry.

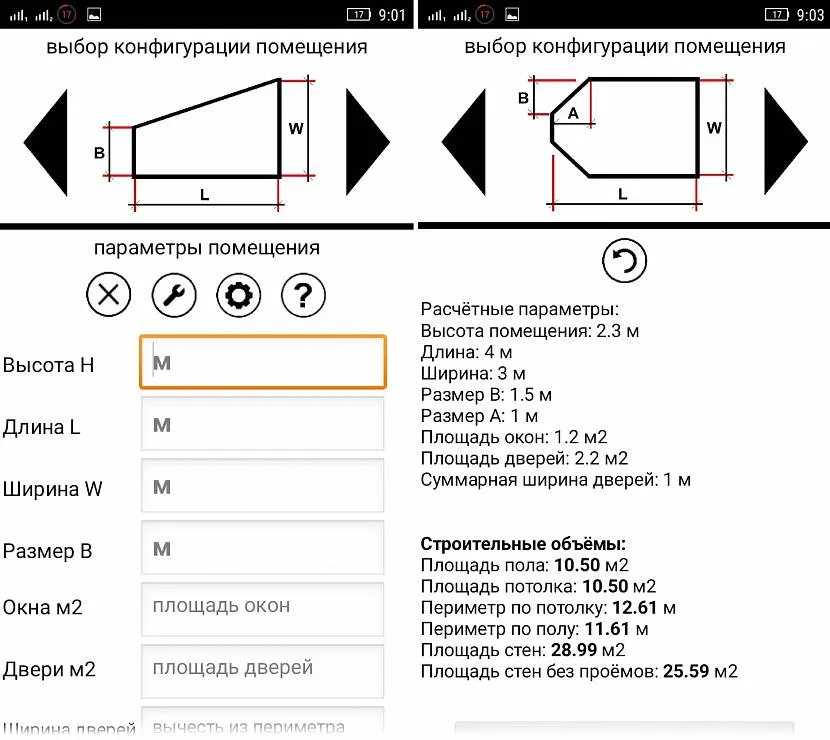
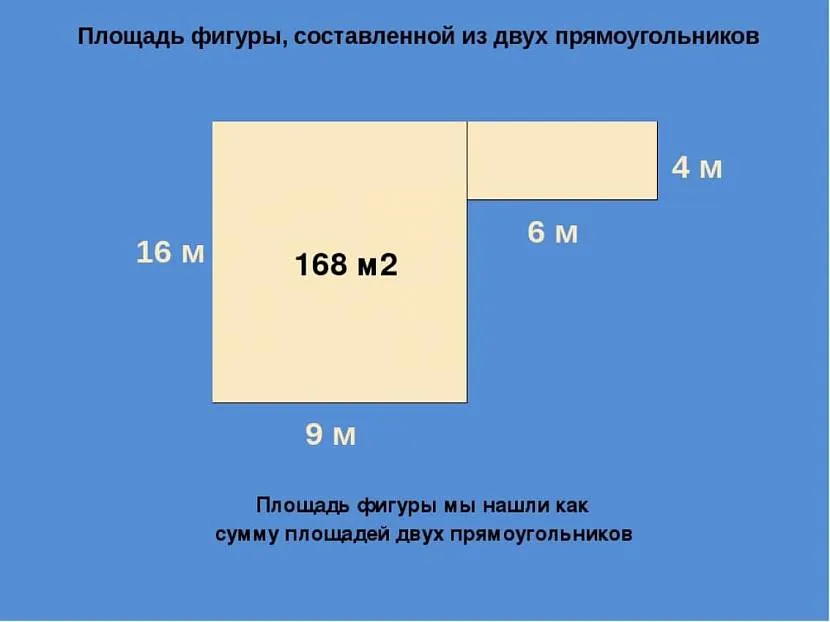
Obliczanie powierzchni złożonej figury
Aby znaleźć wartość powierzchni złożonej figury, musisz najpierw podzielić ją na prostsze kształty geometryczne - trójkąt, prostokąt, kwadrat. Kontury figur powinny mieć wyraźne granice, które się nie nakładają, a jedynie dotykają. Znajdź obszar każdej figury, a następnie zsumuj wyniki.
W prosty sposób możesz znaleźć obszar trójkąta o kącie prostym:
- zmierzyć boki tworząc kąt 90 °;
- pomnóż liczby;
- podziel przez 2 i uzyskaj metry kwadratowe trójkąta.
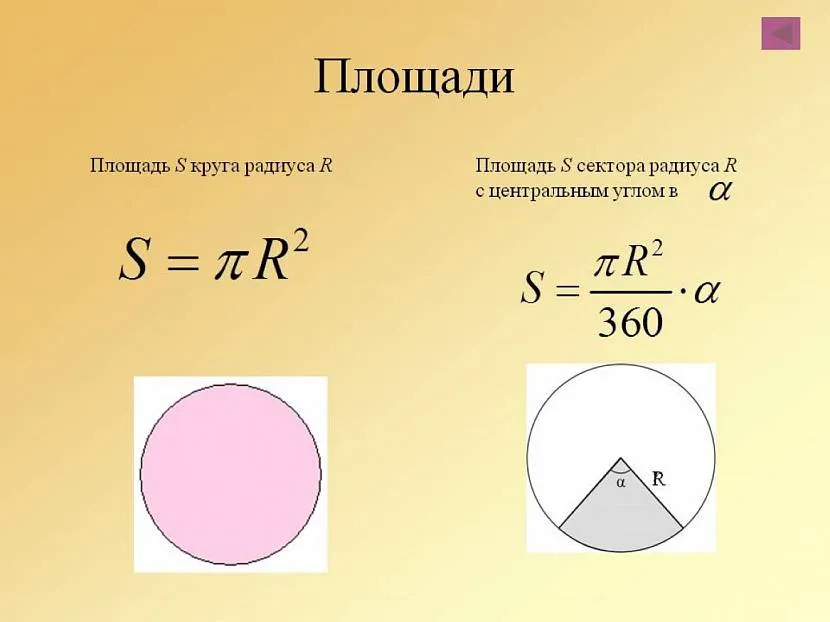
Pozostałe typy trójkątów można rozważyć, wizualnie rysując linię z dowolnego wierzchołka, która tworzy kąt prosty z dowolnej strony. Pole koła można obliczyć za pomocą wzoru: π x R2, gdzie π jest stałą (3.1415926535), a R2 jest cyfrową wartością promienia do drugiego stopnia.
Wniosek
Metr kwadratowy to jednostka powierzchni, numeryczna cecha samolotu. Aby uzyskać taki parametr, należy pomnożyć liczbę wskazującą długość figury przez liczbę jej szerokości. Bardziej poprawne jest wyrażenie „2 metry kwadratowe”, a nie „3 metry kwadratowe”. Wtedy nikt nie uzna, że jeden z boków obiektu ma 3m.